Trigonometric Triangles
 
© 2009
 
David W. Hansen
 
      In the study of trigonometry, it is customary to derive the eight fundamental identities and the double-angle and half-angle formulas by essentially algebraic and analytic methods with little or no use of pictorial aids. However, it is often instructive to represent the six trigonometric functions pictorially as lengths of sides of triangles and to use these “trigonometric triangles” to derive all eight fundamental identities and the double and half-angle formulas. Here’s how we can do it.
 
        Given a right triangle ABC as shown in figure 1 below,                            
                    
                                
the six trigonometric functions of an angle A are defined as:
 
                                           sin A      =    side opposite to A    /    hypotenuse              =      a / c
 
                                           cos A     =    side adjacent to A    /    hypotenuse              =      b / c
 
                                           tan A      =    side opposite to A    /    side adjacent to A    =     a / b
 
                                           cot A      =    side adjacent to A   /    side opposite to A    =      b  / a
 
                                           sec A     =           hypotenuse       /    side adjacent to A     =     c  / b
 
                                           csc A     =           hypotenuse       /    side opposite to A     =     c  / a
 
    To find the values of these six functions and to prove the eight fundamental identities by geometric construction, we first construct angle A.
                                                                   
 Next, we construct a line perpendicular to the angle’s initial side at its vertex.
 
 
                                                    
    Figure 3
 
 
We now draw a line OR of unit length along the terminal side of the angle.
 
 
                                                  
Figure 4
 
 
Dropping the perpendicular from R to the initial side of the angle, we get
 
 
                                                       
Figure 5
 
 
Note: In Figure 5, sin A = XR / OR = XR / 1 = XR. Thus, XR represents sin A, and its length is the value of sin A.
cos A = OX / OR = OX / 1 = OX. Thus, OX represents cos A, and its length is the value of cos A. 
 
    Laying off a line segment OX1 of unit length along the initial side of the angle and constructing X1R1 perpendicular to the initial side of the angle, we get             
                                                           
   Figure 6
 
 
Note: In Figure 6, tan A = X1R1 / OX1 = X1R1 / 1 = X1R1. Thus, X1R1 represents tan A, and its length is the value of tan A. In figure 7 below, sec A = OR1 / OX1 = OR1 /1 = OR1. Thus, OR1 represents sec A, and its length is the value of sec A. 
                                                           
Figure 7
 
    Furthermore, in Figure 7,
 
          1)  Triangle OXR is a right triangle by construction so that OX2 + XR2 = OR2, or
 
                                                                     cos2 A + sin2 A = 1.                                                               (1)
 
          2)  Triangle OX1R1 is a right triangle so that OX12 + X1R12 = OR12, or
 
                                                                     1 + tan2 A = sec2 A.                                                               (2)
 
           3)  Triangle OXR is similar to Triangle OX1R1 so that
 
                   a)     X1R1 / OX1 = XR / OX, or
 
                                 tan A / 1 =  sin A / cos A,        or           tan A   =   sin A / cos A                                  (3)
 
 
                   b)     OR1 / OX1 = OR / OX, or
 
                                 sec A / 1 = 1 / cos A,              or           sec A   =   1 / cos A                                       (4)
     
     Returning to Figure 5, we lay off a line segment OY of unit length along the vertical line perpendicular to OX. Then, we construct YR2 perpendicular to OY and intersecting the terminal side of the angle at R2, giving us             
                                                
Figure 8
 
 
Since YR2 is parallel to OX1, we have  РOR2Y  =  РR2OX1  = Ð A, giving us
 
                                              
Figure 9
 
 
Now, in Figure 9, triangle OYR2 is a right triangle, so cot A = YR2 / OY = YR2 / 1   = YR2. Thus, YR2 represents
cot A, and its length is the value of cot A. 
 
     Dropping a perpendicular line from R2 intersecting the initial side of angle A at X2, we get
 
                                                 
Figure 10
 
which shows that cot A = OX2.   Relabeling Figure 10, we get
 
 
                                            
 
Figure 11
                  
 
From triangle OYR2 in Figure 11, we have csc A = OR2 / OY = OR2 / 1 = OR2. Thus, OR2 represents csc A, and its length is the value of csc A.
 
    Furthermore,
 
          1) Triangle OYR2 is a right triangle by construction so that OY2 + YR22 = OR22, or
 
                                                                     1 + cot2 A = csc2 A.                                                               (5)
 
          2) Triangle OXR is similar to Triangle OX2R2 so that
 
                   a)     OR2 / X2R2 = OR / XR, or
 
                                 csc A / 1 = 1 / sin A,        or           csc A   =   1 / sin A                                               (6)
 
                   b)     OX2 / X2R2 = OX / XR, or
 
                                 cot A / 1 =  cos A / sin A,              or           cot A   =   cot A / sin A                             (7)
 
          3) Triangle OX1R1 is similar to Triangle OX2R2 so that
 
                   a)     OX2 / X2R2 = OX1 / X1R1, or
 
                                 cot A / 1 = 1 / tan A,        or           cot A   =   1 / tan A                                                (8)
 
          Putting all this together, we have Figure 12 below.
 
                                                                                  
Figure 12
                                                                              
     To find the double and half-angle formulas for an angle A, we construct Figure 13 below, where we have drawn unit line segments OX1 and OR along the initial and terminal sides of  Ð X1OR  =  Ð A, respectively.
Then, we have drawn a line segment from R to X1, a line segment RX perpendicular to the initial side of A ,and a  line segment OH which bisects angle A at O, intersecting RX1 at H.     
                                                   
  
Figure 13
 
Now, in figure 14 below, we shall label Ð XRX1 as angle B and show that B =  A/2. This is so because
Triangle ORX1 is an isosceles triangle (OR = OX1 = 1) and thus OH, which bisects angle A, is the perpendicular bisector of RX1. Then, OX1 (the initial side of angle A/2) is perpendicular to RX (the initial side of angle B) and OH (the terminal side of A/2) is perpendicular to RX1 (the terminal side of B), making  B  =  A/2, or
 
                                                                                    A = 2B                                                                      (9)
                                                                      
Figure 14
 
Note that cos A = OX/OR = OX/1 = OX and that OX1 - OX   = 1 - cos A as shown.
 
     In Figure 15 below, we see that Triangle OHR is a right triangle and sin A/2 = HR/OR = HR/1 = HR. And since OH is the perpendicular bisector of RX1, then HR = HX1, or RX1 = 2HR = 2 sin A/2 = 2 sin B.
 
                                             
                                                                                        Figure 15
 
  Now for the double-angle formulas, we see that in Triangle RXX1,  cos B  =  sin A / 2 sin B, or 
sin A  =  2 sin B cos  B.  From (9) above, we have A = 2B, giving us the double-angle formula for the sine function
 
                                                                  sin 2B  =  2 sin B cos B                                                                (10)
 
Also in Triangle RXX1,  sin B  =  (1 - cos A) / 2 sin B, or   2 sin2 B  =  1 - cos A, or  cos A  =  1 - 2 sin2 B.
Using A = 2B from (9), we get
                                                                  cos 2B  = 1 - 2 sin2 B,                                                                   (11)
 
which is one of the double-angle formulas for the cosine function.
 
     For the half-angle formulas, note that in Triangle RXX1,
 
                                                          RX12   =    RX2 + XX12,     or
 
                                                                     =    sin2 A + (1 - cos A)2
 
                                                                     =    sin2 A + 1 - 2 cos A + cos2 A
 
                                                                     =      2 - 2 cos A   [ using (1) ].
                                                                             ___________ 
Hence,                                                RX1   =   √ 2 - 2 cos A .
 
     Thus, in Triangle RXX1,   
 
     a)                                           sin B   = sin A/2 = XX1 / RX1
                                                                                           ___________
                                                               = (1  -  cos A) / √ 2 - 2 cos A , and by rationalizing the denominator
                                                                    ____________
and using (9), we have            sin A/2  = √ (1  -  cos A) / 2 ;                                                                       (12)
 
 
     b)                                           cos B    =   cos A/2 = RX / RX1
                                                                                    ___________
                                                                =    sin A / √ 2 - 2 cos A , and by rationalizing the denominator and
                                                                      ____________
using (9), we have                     cos A/2 = √ (1 + cos A) / 2 ;                                                                       (13)
 
 
     c)                                            tan B    =   tan A/2  =  XX1 / RX
   
                                                                 =   (1  -  cos A) / sin A ,
                                                                    
and using (9), we have               tan A/2  =   (1  -  cos A) / sin A ;                                                                 (14)
 
which are the half-angle formulas for the sine, cosine, and tangent functions.
 
 
     To find the addition formulas for the sine, cosine, and tangent functions, we start with angles A and B added together as shown below in Figure 16. 
                       
Figure 16
 
 
     Next we drop a perpendicular line segment DC from the terminal side of angle B to the initial side of angle A and a perpendicular line segment DE from the terminal side of angle B to the terminal side of angle A as shown below in Figure 17.
                                      
Figure 17
 
 Note: Since DC is perpendicular to OC and DE is perpendicular to OE, then  Ð CDE  =  Ð COE  =  angle A.
 
      Finally, as shown in Figure 18 below, we drop a perpendicular line segment EF from E to the initial side of angle A and a perpendicular line segment EG from E to DC.                               
                                                                         
                                                                                      Figure 18
 
     Then,                        CG   =   EF,        and       CF = GE      and                                                             (15)   
 
 in Triangle OFE,         sin A = EF / OE            or            EF = OE sin A                                                      (16)
                                    cos A = OF / OE           or           OF = OE cos A ;      and                                       (17)
                                     tan A = EF / OF                                                                                                        (18)
       
  in Triangle OED,        sin B = DE / OD           or            DE = OD sin B                                                     (19)
                                    cos B = OE / OD          or            OE = OD cos B ,     and                                       (20)
                                     tan B = DE / OE                                                                                                        (21)
 
  in Triangle DGE,         sin A = GE / DE           or            GE = DE sin A                                                      (22)
                                     cos A = GD / DE          or            GD = DE cos A                                                     (23)
 
                                                           CD                           CG + GD                      
  Now,            sin (A + B)       =      ------------     =          -----------------------   
                                                           OD                                 OD                              
 
                                                                                            EF + GD
                                                                           =          -----------------------                                from (15),
                                                                                                  OD
 
                                                                                     OE sin A   +   DE cos A  
                                                                           =      -----------------------------------                 from (16) and (23),
                                                                                                    OD
 
                                                                      (OD cos B) sin A   +   (OD sin B) cos A  
                                                           =      --------------------------------------------------------        from (20) and (19),
                                                                                                    OD
 
                                                                           OD (cos B sin A   +   sin B cos A)  
                                                           =            ------------------------------------------------   
                                                                                                    OD
 
   Thus,       sin (A + B)                       =                   sin A cos B + cos A sin B.
 
 
                                                         OC                           OF - CF                      
   Also,        cos (A + B)       =      ------------     =          -----------------------   
                                                         OD                                 OD                              
 
                                                                                          OF - GE
                                                                         =          -----------------------                                from (15),
                                                                                                OD
 
                                                                                   OE cos A   -   DE sin A  
                                                                        =      -----------------------------------                 from (17) and (22),
                                                                                                  OD
 
                                                                    (OD cos B) cos A   -   (OD sin B) sin A  
                                                         =      --------------------------------------------------------        from (20) and (19),
                                                                                                  OD
 
                                                                         OD (cos B cos A   -   sin B sin A)  
                                                         =            ------------------------------------------------   
                                                                                                  OD
 
   Thus,      cos (A + B)                     =                   cos A cos B - sin A sin B.
 
 
                                                         CD                           CG + GD                       
   Finally,      tan (A + B)       =      ------------     =          -----------------------   
                                                         OC                           OF   -   CF                              
 
                                                                                          EF + GD
                                                                         =          -----------------------                                from (15),
                                                                                          OF -   GE
 
                                                                                           EF        GD
                                                                                         ------  +  ------
                                                                                           OF        OF
                                                                         =         ----------------------------                        dividing by OF,
                                                                                           OF         GE
                                                                                          ------   -  -------
                                                                                           OF         OF
 
                                    GD                                             DE cos A                                        DE
                     tan A +   ------                          tan A +   -----------------                 tan A +     --------
                                     OF                                            OE  cos A                                       OE
   =          -----------------------------      =     -------------------------------------    =    ------------------------------------        
                                   GE                                             DE sin A                                         DE               
                         1   -   -------                             1     -   -----------------                    1     -       ------   tan A
                                     OF                                            OE cos A                                        OE
 
                                                                                                                          
                      tan A  +    tan B                             tan A    +    tan B                             
    =          -----------------------------------      =     -------------------------------------                    from (21).                     
                         1  -   tan B tan A                          1    -    tan A tan B
 
                                                         tan A + tan B
   Thus,      tan (A + B)     =       -----------------------------    .
                                                       1 - tan A tan B
 
 

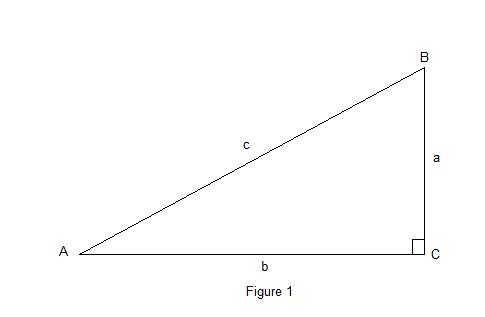
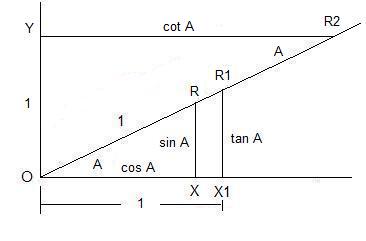
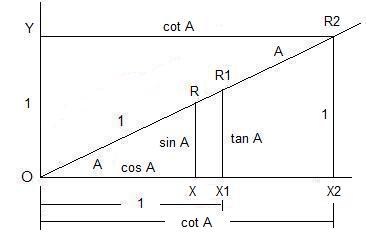
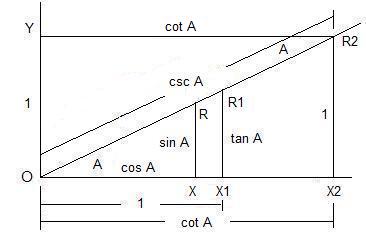
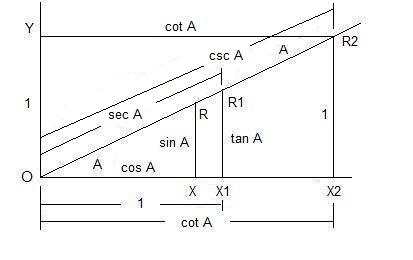
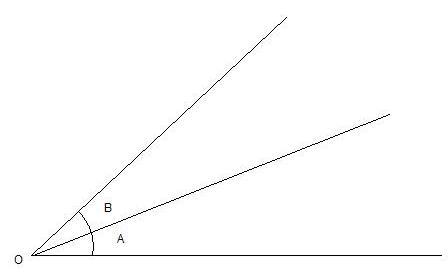
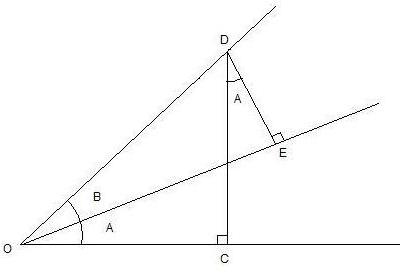
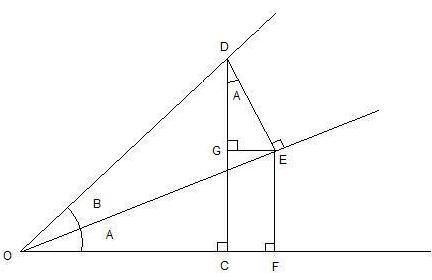
     To find the subtraction formulas for the sine, cosine, and tangent functions, we start with angles A and B subtracted as shown below in Figure 19,

                                             

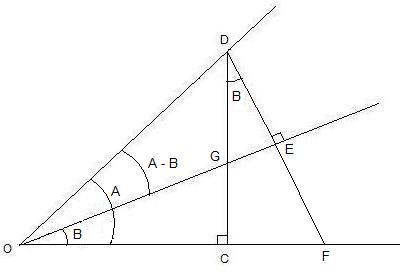
                                                                                          Figure 19

 

with Ð DOC  =  A, Ð GOC  =  B, and Ð DOE = A - B, where we have dropped a line segment DC from the terminal side of angle A perpendicular to the initial side of angle B at C intersecting the terminal side of angle B at G and a line segment DF from the terminal side of angle A perpendicular to the initial side of angle A - B at E intersecting the initial side of angle B at F.

 

Note: Since DC is perpendicular to OF and DF is perpendicular to OE, then Ð GOC  = Ð GDE = angle B.

                                

Also, since DC  =  DG  +  GC, then  DG  =  DC  -  GC                                                                                      (24)

 

In  Triangle OCD,         sin A   =  DC / OD          or            DC  =  OD sin A                                                    (25a)

                                    cos A   =  OC / OD          or           OC  =   OD cos A                                                  (25b)

     and                          tan A   =  DC / OC.                                                                                                       (25c)

       

In  Triangle OCG,         sin B  =  GC / OG          or             GC  =  OG sin B                                                    (26a)

                                    cos B  =  OC / OG          or             OC  =  OG cos B ,                                                (26b)

      and                        tan B   =  GC / OC.                                                                                                        (26c)

 

               Thus, from (25b) and (26b), we have           OG cos B  =  OD cos A                                                 (27)

 

In  Triangle DEG,         cos B  =  DE / DG         or            DE  =  DG cos B                                                       (28)

 

                                                                             DE                           DG cos B                       

Now, in  Triangle OED,    sin (A - B)       =      ------------     =          -----------------------                                 from (28),   

                                                                             OD                                OD                              

 

                                                                                        (DC - GC) cos B

                                                                           =         ------------------------                                                from (24),

                                                                                                  OD

 

                                                                                    (OD sin A  -  OG sin B) cos B

                                                                           =    ------------------------------------------             from (25a) and (26a),

                                                                                                    OD

 

                                                                         OD sin A cos B  -  (OG cos B)sin B 

                                                           =      --------------------------------------------------------                          regrouping,

                                                                                                    OD

 

                                                                           OD sin A cos B  -  OD cos A sin B    

                                                           =            --------------------------------------------------                             from (27),   

                                                                                                    OD

 

Thus,          sin (A - B)                       =                   sin A cos B  -  cos A sin B.

 

In  Triangle OEF,       cos B   =   OE / OF          or            OE  =  OF cos B                                                      (29)

       

In  Triangle DCF,         sin B  =  CF / DF            or             CF  =  DF sin B                                                      (30a)

                                    cos B  =  DC / DF           or             DC  =  DF cos B ,                                                  (30b)

      and                        tan B   =  CF / DC.                                                                                                          (30c)

 

                                                                            OE                           OF cos B                      

Now, in Triangle OED,   cos (A - B)       =      ------------     =          -----------------------                                   from (29),

                                                                            OD                                 OD                               

 

                                                                                          (OC + CF) cos B

                                                                         =             --------------------------

                                                                                                    OD

 

                                                                                   (OD cos A + DF sin B) cos B 

                                                                         =      -----------------------------------------                 from (25b) and (30a),

                                                                                                    OD

 

                                                                    OD cos A cos B   +   (DF cos B) sin B  

                                                         =      --------------------------------------------------------                              regrouping,

                                                                                                  OD

 

                                                                         OD cos A cos B   +   DC sin B  

                                                         =            ------------------------------------------------                                   from (30b),

                                                                                                  OD

 

                                                                         OD cos A cos B   +   (OD sin A) sin B  

                                                         =            ------------------------------------------------                                   from (25a),

                                                                                                  OD

 

Thus,           cos (A  -  B)                    =                   cos A cos B  +  sin A sin B.

 

                                                                         DE                           DG cos B                      

And, in Triangle OED,  tan (A - B)       =      ------------     =          -----------------------                                      from (28),   

                                                                         OE                               OE                              

 

                                                                                        (DC - GC) cos B

                                                                         =          -----------------------                                         from (24) and (29),

                                                                                            OF cos B

 

                                                                                          DC - GC

                                                                          =            --------------

                                                                                              OF

 

                                                                                           DC - GC

                                                                           =             ---------------

                                                                                           OC + CF

 

 

                                                                                           DC       GC

                                                                                          ------  -  ------

                                                                                           OC       OC

                                                                         =         ----------------------------                                      (dividing by OC)                                                                                            OC         CF

                                                                                          ------   +  -------

                                                                                           OC         OC

 

                                                                                                                                 

                                                                                            tan A   -   tan B               

                                                                          =          -----------------------------                           from (25c) and (26c),   

                                                                                                      DC      CF                                             

                                                                                           1  +    ------ • -------                            

                                                                                                      OC      DC                           

                                                                                                                                                                                           

                                                                                            tan A   -   tan B                                 

Thus,                 tan (A  -  B)                              =          ------------------------------                        from (25c) and (26c)                                                                                                 1    +   tan A tan B                            

 

                                                                              OE                                 OE                     

Finally, in Triangle OED,   cot (A - B)       =      ------------     =          -----------------------                               from (28),   

                                                                              DE                            DG cos B                                        

 

                                                                                            OF cos B

                                                                         =          -----------------------                                      from (24) and (29),

                                                                                      (DC - GC) cos B

 

                                                                                                OF 

                                                                          =              --------------

                                                                                            DC - GC

 

                                                                                            OC + CF

                                                                           =             ---------------

                                                                                            DC - GC

 

                                                                                             OC       

                                                                                            -------    +   1                                                 

                                                                                              CF       

                                                                           =             ---------------------                                    (dividing by CF)

                                                                                             DC         GC

                                                                                            ------   -   ------

                                                                                             CF          CF

 

 

                                                                                             OC       DC

                                                                                            ------  •  ------   +  1

                                                                                             DC        CF

                                                                         =         --------------------------------              

                                                                                                                GC                                                                                                   

                                                                                              cot B    -   ---------           from Triangle  DCF in Figure 19,

                                                                                                                 CF

 

               GC             GC         OC        DC            GC          DC        OC          

Now,    --------   =    -------   •   --------   •   --------     =     --------   •   --------   •   --------      =     tan B cot B cot A    =   cot A      (31) 

               CF              CF         DC        OC            OC          CF         DC

 

                                                                                           cot A cot B  +  1                     

    Thus,                     cot (A - B)                        =           -----------------------------                          substituting from (31). 

                                                                                             cot B   -   cot A                                     

                                                                                                                                

 
References
 
 
        [1] Hansen, David W., Trigonometric Triangles, Mathematics in College, City University of New York,
                                Spring-Summer 1986, pp. 32-36.
 
 
 
                                                                                       Home