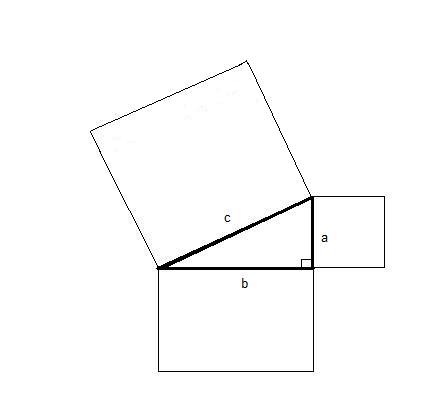
Now, angle 1 in the upper right triangle is equal to angle 1 in the lower right triangle because corresponding angles of congruent triangles are equal. Also, in the lower right triangle
angle 1 + angle 3 = 90o (1)
because they are complementary angles of a right triangle. Since angles 1, 2, and 3 form a straight angle, we get
angle 1 + angle 2 + angle 3 = 180o
angle 2 + (angle 1 + angle 3) = 180o, (regrouping)
angle 2 + 90o = 180o. (substituting from (1) above)
and, angle 2 = 90o. (subtracting 90o from both sides of the equation)
So, angle 2 is a right angle, and we can show in the same way that the other three angles in the interior quadrilateral are also right angles. This proves that the quadrilateral inside the larger square is itself a square.
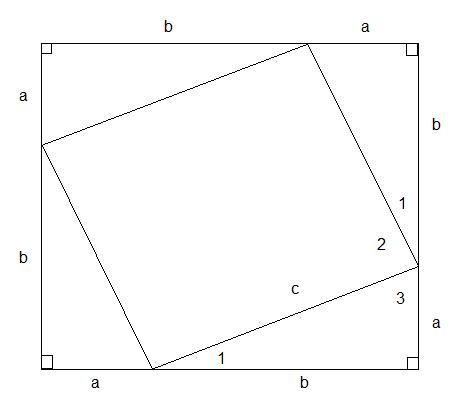
Now, for the fun! From figure 2 we see that the area of the larger square is equal to the sum of the areas of the four interior right triangles and the smaller interior square. Since a + b is the length of one side of the larger square, (1/2)ab is the area of one of the four right triangles , and c is the length of one side of the smaller square, we get:
Area of the larger square = Area of the 4 triangles + the Area of the smaller square, or
(a + b)2 = 4(1/2)ab + c2,
a2 + 2ab + b2 = 2ab + c2,
and a2 + b2 = c2. (subtracting 2ab from both sides)
thus proving the Pythagorean Theorem.
2. Finding Right Triangles with Integral Sides
In section 1 above, we proved the Pythagorean Theorem for all right triangles, where a, b, and c are certain real numbers, not necessarily integers. However, are there any right triangles with sides whose lengths are positive integers only? The answer is a resounding YES! Now, of course, not just any three positive integers will do! For example, if a = 2, b = 6, and c = 7, then a2 + b2 = 22 + 62 = 40, whereas c2 = 72 = 49. Thus, a2 + b2 does not equal c2, and there is NO right triangle with sides of 2, 6, and 7. However, if a = 3, b = 4, and c = 5, then a2 + b2 = 32 + 42 = 25, and c2 = 52 = 25. Here, a2 + b2 DOES equal c2. This tells us that a right triangle with sides of lengths 3, 4, and 5 does exist.
Now, a set of three positive integers a, b, and c, which satisfies the equation a2 + b2 = c2, is called a Pythagorean triple and is written (a, b, c). Thus, (3,4,5) is a Pythagorean triple and (2,6,7) is not. The three integers in a Pythagorean triple, of course, can be thought of as the lengths of the two legs and hypotenuse of a right triangle, and vice-versa. In fact, whenever something is true of a Pythagorean triple, it is also true of a right triangle with integral sides.
Are there other Pythagorean triples? Again, the answer is yes. Any multiple of the three integers in a Pythagorean triple will be a Pythagorean triple. Forexample, multiplying each of the three integers in (3,4,5) by 2 gives us (6,8,10), which is a Pythagorean triple since 62 + 82 = 102. Multiplying by 3, we get (9, 12, 15), which is also a Pythagorean triple since 92 + 122 = 152. In fact, if (a, b, c) is a Pythagorean triple (and thus a2 + b2 = c2 ), then multiplying each of its integers by any positive integer n gives us (na, nb, nc), another Pythagorean triple, since
(na)2 + (nb)2 = n2 a2 + n2 b2 = n2(a2 + b2) (factoring)
= n2 c2 (replacing a2 + b2 by c2 )
= (nc)2, (factoring)
proving that (na)2 + (nb)2 = (nc)2 , and thus (na, nb, nc) is a Pythagorean triple. Since n can be any positive integer, there will be an infinite number of right triangles with integral sides. This gives us
Theorem 2
If (a, b, c) is a Pythagorean triple and n is any positive integer, then (na, nb, nc)
is a Pythagorean triple, and the number of Pythagorean triples is infinite.
_________________________________________________________________
Now, it is definitely nice to know there are an infinite number of Pythagorean triples, or what is the same thing, an infinite number of right triangles with integral sides. But, if each of a triangle’s sides is simply a multiple of the length of another right triangle’s side, we see at once that these right triangles are similar to each other.
Could we perhaps find other right triangles whose integral sides are NOT multiples of some other right triangle’s sides? That is, could we perhaps find right triangles whose sides have NO common factors; or equivalently, Pythagorean triples whose integers have no common factors? Let’s see.
3. Primitive Pythagorean Triples and Triangles
We shall call a Pythagorean triple which has NO common factors a primitive Pythagorean triple. (Similarly, a right triangle with integral sides which have NO common factors will be called a primitive right triangle.) Thus,
(3, 4, 5) is a primitive Pythagorean triple because its integers have no common factors, whereas (6,8,10) is not, since it has a common factor of 2. Note that if any two integers in a Pythagorean triple have a common factor, then the third integer in the triple will also. Here’s why.
Definition: r is a factor (or divisor) of an integer n if there exists an integer s such that n = rs. We also say that n is divisible by r.
Example a) 12 has a factor of 3 because there exists an integer s (namely 4) such that 12 = 3(4).
b) 8 is not divisible by 5 because there is no integer s such that 8 = 5s.
c) 7 is a divisor of 42 because there exists an integer s (namely 6) such that 42 = 7(6).
Now, suppose a and b have a common factor f. Then, a and b can be written as a = fg and b = fh for some integers g and h. Then, since a2 + b2 = c2, we have
(fg)2 + (fh)2 = c2 , f2g2 + f2 h2 = c2, f2 (g2 + h2 ) = c2,
g2 + h2 = c2/f2, and g2 + h2 = (c/f)2.
Look at this last equation. Its left-hand side is an integer, since g and h are integers. So, (c/f)2 is an integer,
and thus c/f must be an integer, for if not, its square could not be an integer. Thus, c/f is some integer, say k. Then, c/f = k, or c = fk, showing that f is a factor of c and thus, f is a common factor of a, b, and c. A similar proof holds if a and c have a common factor, or if b and c do. We have proved the following theorem.
Theorem 3
If any two integers in a Pythagorean triple have a common factor,
then the third integer has that factor also.
_____________________________________________________
Now, are there any primitive Pythagorean triples? Certainly (3,4,5) is one, since 3, 4, and 5 have no common factors. Any others? Let’s see. By trial-and-error, we can find (5,12,13) and (7,24,25). But, surely there must be some easier and more efficient way to find primitive Pythagorean triples than by mere guesswork!
4. A Generating Formula for Primitive Pythagorean Triples
Formulas for generating some primitive Pythagorean triples have been known since Babylonian times, but it was Euclid who, in his Elements, presented the first formula for generating all primitive Pythagorean triples. Our proof of it here follows closely the one given in [2]. But first, we must prove the following preliminary facts.
a) An integer n is even if it has a factor of 2. Thus, it can be written as n = 2k for some integer k. 10 is even because we can find the integer k = 5 such that 10 = 2(5).
b) An integer n is odd if it is one greater than some even integer. Thus, it can be written as n = 2k + 1 for some integer k. 63 is odd because we can find the integer k = 31 such that 63 = 2(31) + 1.
c) The sum (or difference) of two even integers is an even integer, for let r = 2j and s = 2k be two even integers. Then, r ± s = 2j ± 2k = 2(j ± k), which shows that r ± s has a factor of 2 and is thus even.
d) The sum (or difference) of two odd integers is an even integer, for let r = 2j+1 and s =2k+1. Then,
r + s = (2j+1) + (2k + 1) = 2j + 2k + 2 = 2(j + k + 1), which shows r + s has a factor of 2 and is thus even. Similarly, r – s = (2j + 1) – (2k + 1) = 2j + 1 – 2k – 1 = 2(j – k), showing that r - s has a factor of 2 and is thus even.
e) The sum (or difference) of an odd integer and an even integer is an odd integer, for let r = 2j + 1 and
s = 2k. Then, r ± s = (2j + 1) ± 2k = 2j ± 2k + 1 = 2(j ± k) + 1, showing that r ± s is one greater than an even integer and is thus odd.
f) The square of an even integer is even, for let r = 2j, an even integer. Then, r2 = (2j)2 = 4j2 = 2(2j2), which shows that r2 has a factor of 2, and is thus even.
g) The square of an odd integer is odd, for let r = 2j + 1, an odd integer. Then, r2 = (2j + 1)2 = 4j2 + 4j + 1 =
2(2j2 + 2j) + 1, which shows that r2 is one greater than an even integer and is thus odd.
h) Note that if r2 is even, then r is even, for if r were odd, then r2 would have to be odd by g) above. But r2 is even. Similarly, if r2 is odd, then r is odd, for if rwere even, then r2 would have to be even by f) above. But r2 is odd.
Now we’re ready to consider the three integers a, b, and c of a primitive Pythagorean triple, remembering this means the three integers have no common factors.
1. Can a, b, and c all be even integers? No, for then each of them would have a common factor of 2. But they
have no common factors, so a, b, and c cannot all be even.
2. Can a, b, and c all be odd integers? No, for if they were, then a2, b2, and c2 would all be odd and a2 + b2
would be even, since it is a sum of two odd integers. Then, since c2 = a2 + b2, c2 would also be even. But, this is
a contradiction because we assumed that c2 is odd! So, a, b, and c cannot all be odd.
3. a and b cannot both be even, for if they were, then a and b would have a common factor of 2 and by
Theorem 3, c would also, and thus all three integers would have a common factor of 2. But, a, b, and c have no
common factors.
4. a and b cannot both be odd, for if they were, then c would have to be even, because we found in 2, above,
that not all of the integers can be odd. Letting c = 2p, a = 2j + 1, and b = 2k + 1, for some integers p, j, and k, we
get c2 = (2p)2 = 4p2, which has a factor of 4, but, a2 + b2 = (2j + 1)2 + (2k + 1)2 = 4j2 + 4j + 1 + 4k2 + 4k
+ 1 = 4j2 + 4j + 4k2 + 4k + 2, which does NOT have a factor of 4. (Although 4 is a factor of the first four terms in
the underlined expression above, it certainly is not a factor of the fifth term, 2.) Thus, a2 + b2 cannot equal c2,
and our assumption that both a and b are odd is false.
The only possibility remaining is that one of the a or b must be odd and the other even. We say then that these integers are of opposite parity, and for convenience, we shall always pick a to be odd and b to be even.
Now, if a is odd and b is even, then a2 is odd, b2 is even, and thus a2 + b2 is odd. So, c2 is odd since a2 + b2 = c2, and c is odd also. This gives us
Theorem 4
In a primitive Pythagorean triple (a, b, c), a and b are of opposite parity
(one must be odd and the other even), and c is odd.
___________________________________________________________
In summary, for any primitive Pythagorean triple (a, b, c) or primitive right triangle, we have that a is odd, b is even, and c is odd, and no two of the integers a, b, and c have any common factors, for if they did, then all three would have a common factor (by Theorem 3), and the triple would not be primitive.
Now, for any primitive Pythagorean triple (a, b, c), we have a2 + b2 = c2,
or b2 = c2 - a2 = (c + a) (c - a).
Since both a and c are odd, then c + a and c - a are even, and are thus both divisible by 2. So, (c + a)/2 and (c - a)/2 are both integers even though written in the form of apparent fractions. Furthermore, (c + a) 2 and (c - a)/2 have NO common factors! Let’s see why.
If both (c + a) / 2 and (c - a) / 2 have a common factor, say f, then we can find integers g and h so that (c + a) / 2 = fg and (c - a) / 2 = fh. Multiplying both of these equations by 2, we get
c + a = 2fg
and c - a = 2fh.
Adding these equations gives us 2c = 2fg + 2fh,
or c = f(g + h), showing us that f is a factor of c.
Subtracting these two equations gives us.
2a = 2fg - 2fh,
or a = f(g - h), showing us that f is a factor of a.
Thus, f is a factor of both a and c! But, this is impossible since a and c have NO common factors. Thus,
(c + a)/2 and (c - a)/2 have NO common factors. Amazing!
Now, dividing both sides of b2 = c2 - a2 by 4, we get b2 / 4 = (c2 - a2 ) / 4,
or (b / 2)2 = [(c + a) / 2] [(c - a) / 2] .
If we let D = (c + a) / 2 and E = (c - a) / 2 (1a)
then we get (b / 2)2 = DE, (1b)
where D and E are integers which have NO common factors.
Look carefully at equation (1b). Its left-hand side, (b/2)2, is a perfect square, so its right-hand side, DE, must also be a perfect square. Furthermore, D and E must have NO common factors. Can we deduce anything about D and E from this information? Let’s look at an example.
Suppose b = 12. Then, b/2 = 6, and (b/2)2 = 36. Then, the possible values for D and E which make (1b) true are (b/2)2 = 36 = 1(36) = 2(18) = 3(12) = 4(9) = 6(6) = DE, and we see that the only values for D and E which have no common factors are those in which D and E are both themselves perfect squares; namely, 1(36) and 4(9). This suggests that in general, D and E must always be perfect squares. Here’s why.
Since b is even, b has a factor of 2. So, b/2 is an integer and is either a prime or a product of the powers of its prime factors. Then, (b/2)2 will be a product of the squares of the powers of its prime factors. Let’s look at an example.
1. Let b = 240. Then, b/2 = 120 = 8(15) = 23(3)(5), and (b/2)2 = (23)2(32)(52), which certainly is a product of the squares of the powers of its prime factors. Simplifying, we get
(b/2)2 = 26(32)(52) = DE. (2)
Now, we have just proved that D and E on the right-hand side of (2) have no common factors, so some possible factors for D and E are a) D = 26(32) and E = 52 or b) D = 32 and E = 26(52 ), but since D and E have no common factors, they could not have factors such as c) D = 23(32) and E = 23(52) or d) D = 24(3) and E = 22(3)(52), since in c), 23 is a common factor, and in d), 22(3) is a common factor.
Notice that each separate power of a prime factor (like 26 or 32 or 52) appears completely and entirely in either D or E but not both, or else D and E would have a common factor. Thus, D and E must each consist of the product of the squares of powers of the prime factors of (b/2)2, and nothing else. So, D and E must both be squares themselves!
Thus, for some positive integers m and n, we can let
D = m2 and E = n2. (3)
Substituting the values of D = (c + a)/2 and E = (c - a)/2 from (1a) above into (3), we get
(c + a)/2 = m2 and (c - a)/2 = n2. (4)
Multiplying these last two equations by 2, we get c + a = 2m2 (5)
and c - a = 2n2. (6)
Adding equations (5) and (6) gives us 2c = 2m2 + 2n2,
or c = m2 + n2. (7)
Subtracting equation (6) from (5), we get 2a = 2m2 - 2n2,
or a = m2 - n2. (8)
Finally, from (1b) above, we have (b/2)2 = DE, and substituting for D and E from (3) above,
we get (b/2)2 = m2n2, or b2/4 = m2n2.
Taking the square root of both sides of this last equation, we get b/2 = mn, or b = 2mn. (9)
Summarizing, (7), (8), and (9) tell us that if (a, b, c) is any primitive Pythagorean triple, then formulas for finding the values of a, b, and c are given by
a = m2 - n2, b = 2mn, c = m2 + n2
for positive integers m and n. However, . . .
1. So that a will be positive, we must have m > n.
2. m and n must have NO common factor, or else a, b, and c would also have that same common
factor, and (a, b, c) would not be primitive.
3. Since a is odd, then a = m2 - n2 must be odd, also. But, if m and n are both odd or both even, then m2 - n2 will
be even. So, one of m and n must be odd and one must be even. In other words, m and n must be of opposite
parity.
Well, there it is! We have here a most wonderful set of formulas which we can use to compute the values of either primitive Pythagorean triples or their corresponding right triangles.
Now, as summarized above, we started with a given primitive Pythagorean triple and ended up with the equations for the values of a, b, and c. However, what if we start with given values of m and n? Will these values give us a primitive Pythagorean triple (a, b, c)? Let’s see.
First, they definitely give us a Pythagorean triple, for if a = m2 - n2, b = 2mn, and c = m2 + n2,
then a2 + b2 = (m2 - n2)2 + (2mn)2
= m4 - 2 m2n2 + n4 + 4m2n2
= m4 + 2 m2n2 + n2
= ( m2 + n2 )2 = c2.
And, it will be a primitive Pythagorean triple because (a, b, c) will have NO common factors. Let’s see why.
First, since one of the m and n is even and one odd, then one of the m2 and n2 must be even, and the other one odd. Thus, c = m2 + n2 will be odd, and (a, b, c) cannot then have any even common factors.
Second, suppose that (a, b, c) has an odd common factor. Then this factor will have at least one odd prime factor, call it p, and we can find integers f and g such that a = pf and c = pg. Substituting these values for a and c into equations (5) and (6) above, we have
(5) c + a = 2m2 and (6) c - a = 2n2,
or pg + pf = 2m2 and pg - pf = 2n2. and
factoring, p(g + f) = 2m2 and p(g - f) = 2n2.
Now, these last two equations show us that p is a factor of the left-hand sides of the two equations, so p must be a factor of the right-hand sides of the two equations. But p is an odd prime, so it cannot be a factor of the 2. So, p must be a factor of the m2 and n2, and thus a factor of m and n. But m and n have no common factors, so our assumption that (a, b, c) has an odd common factor is false. Thus, (a, b, c) has NO odd common factors.
Since (a, b, c) has no even nor odd common factors, it is thus a primitivePythagorean triple, and so the formulas we have obtained generate ALL primitive Pythagorean triples (and primitive right triangles), thereby proving the following theorem.
Theorem 5 (The Generating Formulas)
Let m and n be positive integers of opposite parity with no common factors
and m > n. Then, for all primitive Pythagorean triples (a, b, c),
a = m2 - n2, b = 2mn, and c = m2 + n2.
______________________________________________________________
Other Proofs of Theorem 5
Here are two other interesting ways to derive the generating formulas of Theorem 5. These are not complete proofs, since they do not consider the restrictions on m and n nor show that the formulas derived will generate all primitive Pythagorean triples.
Proof 1 ( From [3] ) Since a2 + b2 = c2, then b2 = c2 – a2 = (c + a)(c – a). We may rewrite this as
b c – a
---------- = ----------- = k, where k is some fraction, say k = n/m.
c + a b
b c – a
Then, ---------- = k, or b = k(c + a) (1), and ----------- = k, or c – a = kb (2)
c + a b
Rewriting (1) and (2), we get ka – b = - kc (3)
and a + kb = c (4)
Multiplying (3) by k and adding this to (4), we get
k2a – kb = - k2c
a + kb = c
------------------------------ (1 – k2)c
(k2 + 1)a = (1 – k2)c or a = ------------------ (5)
k2 + 1
Multiplying (4) by - k and adding this to (3) gives us
- ka – k2b = - kc
ka – b = - kc
---------------------------- 2kc
( -1 – k2)b = - 2kc or b = ----------------- (6)
k2 + 1
Replacing k by n/m in (5) and (6) and multiplying the numerators and denominators of each fraction by m2 gives us
(1 – n2/m2)c (m2 – n2)c
a = ------------------------- = -------------------- (7)
n2/m2 + 1 m2 + n2
2(n/m)c (2mn)c
b = ------------------------- = ------------------ (8)
n2/m2 + 1 m2 + n2
Since a and b must be integers, we pick c equal to m2 + n2 to make them so. This then gives us
a = m2 – n2, b = 2mn, c = m2 + n2.
Proof 2 ( From [4] ) We know that x2 + 2nx + n2 = (x + n)2.
If we set 2nx + n2 = m2, (1)
we get x2 + m2 = (x + n)2, (2)
which is the sum of two squares equal to a third square.
Solving (1) for x, we get x = (m2 – n2) / 2n, and substituting this value for x into (2) gives us
[ (m2 – n2) / 2n ]2 + m2 = [ (m2 – n2) / 2n + n ]2
= [ (m2 – n2 ) / 2n + 2n2 / 2n ]2
= [ (m2 – n2 + 2n2 ) / 2n ]2 = [ (m2 + n2) / 2n ]2,
or (m2 – n2)2 / 4n2 + m2 = (m2 + n2)2 / 4n2. (3)
Multiplying (3) by 4n2 results in (m2 – n2)2 + 4m2n2 = (m2 + n2)2,
or (m2 – n2)2 + (2mn)2 = (m2 + n2)2.
Comparing this with a2 + b2 = c2, we have a = m2 – n2, b = 2mn, and c = m2 + n2.
5. Properties of Primitive Pythagorean Triples
Let’s use our formulas from Theorem 5 to construct a small table of primitive Pythagorean triples. The values chosen for m and n are those for which m and n have no common factors, are of opposite parity, and m is greater than n.
Table 1. Primitive Pythagorean Triples
a b c Perimeter
m n m2 - n2 2mn m2 + n2 a+b+c
-----------------------------------------------------------------------------------------------------------
2 1 3 4 5 12
3 2 5 12 13 30
4 1 15 8 17 40
4 3 7 24 25 56
5 2 21 20 29 70
5 4 9 40 41 90
6 1 35 12 37 84
6 5 11 60 61 132
7 2 45 28 53 126
7 4 33 56 65 154
7 6 13 84 85 182
8 1 63 16 65 144
8 3 55 48 73 176
8 5 39 80 89 208
8 7 15 112 113 240
9 2 77 36 85 198
9 4 65 72 97 234
9 8 17 144 145 306
10 1 99 20 101 220
-----------------------------------------------------------------------------------------------------------
Looking at this table, can we see any interesting patterns? Well,
First, notice that a and c are always odd, and b is always even. Since m and n are of opposite parity, then both
a = m2 – n2 and c = m2 + n2 will always be odd as they are the difference or sum, respectively, of two integers, one odd and one even. b = 2mn has the factor 2, so it will always be even. Also, since either m or n is even, b will have another factor of 2, thus giving it two factors of 2. So, b will always be divisible by 4, as we may have noticed in the table. Furthermore, note that in the table, c is either a prime or divisible by 5, but this may not be true for ALL triples.
Second, notice that the values for the perimeter are all even. This is so because the perimeter is the sum of two odd integers, a and c (which gives us an even sum), and one even integer, b.
Next, let’s look at the various sums and differences of the a’s, b’s, and c’s. For the first triple (3, 4, 5), we see that a + b = 7, a + c = 8, and b + c = 9. Now, the first two sums are of no great interest, but the third sum, b + c = 9, definitely is, because it is a perfect square! Could this be true of all primitive Pythagorean triples? Stop now and take a good look at Table 1 to see if it is.
It does seem so, doesn’t it?
In the second triple (5, 12, 13), b + c = 12 + 13 = 25 = 52, in the third triple, b + c = 8 + 17 = 25 = 52, in the fourth triple, b + c = 49 = 72, and so on for all the triples in Table 1. For the last triple, (99, 20 101), we have
b + c = 121, which is 112. This is powerful evidence that for any primitive Pythagorean triple, b + c is a perfect square. Now just because it is true for every triple in Table 1, we cannot say it is true for ALL primitive Pythagorean triples. We must prove this without using a table of values, since NO table could ever be large enough to show all primitive Pythagorean triples.
Perhaps the formulas of Theorem 5 can help us. They tell us that
b = 2mn and c = m2 + n2.
Thus, b + c = 2mn + (m2 + n2) = m2 + 2mn + n2 = (m + n)2, (1)
which is, indeed, a perfect square, thus proving that b + c is always a perfect square. While the table was invaluable in helping us to verify our conjecture, the formulas were necessary to actually prove it.
Look again at the first triple (3, 4, 5) in Table 1. Here b + c = 9, a perfect square, and amazingly, its square root, 3, is the value of a. Let’s see if this is true for all triples in Table 1. Looking at the second triple (5,12,13), we see that b + c = 25, and its square root, 5, is indeed the value of a. However, in the third triple (15, 8, 17), b + c = 25, but its square root, 5, is not the value of a. What’s going on?
In (1) above, we proved that b + c = (m + n)2, Ö
_____
so Ö b + c = m + n . (2)
Theorem 5 tells us a = m2 - n2 = (m + n)(m - n), (3)
_____ _____
Now, using (2) to replace m + n in (3) by Ö b + c , we get a = Ö b + c (m - n), (4)
_____
which shows us that Ö b + c is a factor of a.
Now, for some primitive Pythagorean triples, the square root of b + c will not only be a factor of a, but will be
_
exactly equal to a; for example, in (3, 4, 5), 4 + 5 = 9 and Ö9 = 3 = a, and in (11, 60, 61), 60 + 61 = 121, and
___ ____
Ö121 = 11 = a. This is so nice that whenever Ö b+c = a, we shall call the resulting primitive Pythagorean triple
a complete Pythagorean triple.
____ ______ ___
Thus, (13, 84, 85) is a complete Pythagorean triple because Ö b+c = Ö 84 + 85 = Ö169 = 13 = a.
______ ___
However, (21, 20, 29) is not complete since Ö 20+29 = Ö 49 = 7 ≠ a = 21, but 7 is a factor of a.
Now, when will a primitive Pythagorean triple (a,b,c) be complete? In equation (4) above, if m – n = 1,
____ _____ _____
then a = Ö b + c (m - n) = Ö b + c (1) = Ö b + c , and (a,b,c) will be complete. And, if m - n = 1, then
m = n + 1, and using Theorem 5, we have
b = 2mn = 2(n+1)n = 2n2 + 2n
and c = m2 + n2 = (n+1)2 + n2 = 2n2 + 2n + 1,
showing us that c = b + 1.
Thus, (a, b, c) is complete if c = b + 1 (or m = n + 1).
Now, using a = m2 - n2, b = 2mn, and c = m2 + n2, from Theorem 5, and by examining their various additions and subtractions, we find that
c + a = 2m2 (5) and c - a = 2n2, (6)
or (c + a) / 2 = m2 and (c - a) / 2 = n2, so BOTH (c + a) / 2 and (c - a) / 2 are perfect squares!
_________ ________
Furthermore, since Ö (c + a) / 2 = m and Ö (c - a) / 2 = n, they are both factors of b = 2mn.
In addition, from (5), we have (c + a) / b = 2m2 / 2mn = m / n, (7)
and from (6), (c – a) / b = 2n2 / 2mn = n / m. (8)
These last two equations, (7) and (8), are useful in finding the values of m and n for a given primitive Pythagorean triple.
Finally, we have c - b = (m2 + n2) - 2mn = m2 - 2mn + n2 = (m - n)2, which is a perfect square,
and its square root, m - n, is a factor of a = m2 – n2 = (m + n)(m – n). What beautiful patterns we have found!
All this gives us
Theorem 6
In any primitive Pythagorean triple (a, b, c),
1) b + c = (m + n)2 and c - b = (m - n)2, both of which are perfect squares.
Their square roots are factors of a.
2) if c = b + 1, (m = n + 1), then the square root of b + c equals a, and
(a, b, c) is said to be a complete Pythagorean triple.
3) (c + a) / 2 and (c - a) / 2 are perfect squares. Their square roots are
factors of b.
4) (c + a) / b = m / n and (c – a) / b = n / m.
________________________________________________________________
Example 1. Let’s look at the patterns in the triple (5, 12, 13). How beautiful they are!
First, the sum of its last two integers is the perfect square 25, whose square root, 5, is the first integer of the triple, making it complete.
Second, the difference between its last two integers is the perfect square 1, whose square root, 1, is a factor of the first integer.
Third, the sum of the third and first integers, when divided by 2, is the perfect square 9, and its square root, 3, is a factor of the second integer.
Fourth, the difference of the third and first integers, when divided by 2, is the perfect square 4, whose square root, 2, is also a factor of the second integer.
Fifth, the sum of the squares of the first two integers, 52 + 122, equals the square of the last integer, 132.
Finally, the sum of the first and third integers divided by the second integer, (a + c) /b = (5 + 13)/12 = 18/12 = 3/2 = m / n, gives us the values of m and n which generate (5, 12, 13); that is, m = 3 and n = 2.
Truly this is a quite remarkable example of the hidden order and symmetry which is contained within this simple-looking primitive Pythagorean triple!
Example 2. Find a primitive right triangle whose hypotenuse is 25 units longer than its even leg. We have that the hypotenuse c = b + 25, or c - b = 25. From Theorem 6, we know that c - b = (m - n)2, so (m - n)2 = 25, or m - n = 5. Thus, any primitive right triangle for which m - n = 5 (or equivalently, m = n + 5) will have an hypotenuse whose length is 25 units longer than its even leg. There will be an infinite number of them. Listed below are the first four triangles (for n = 1, 2, 3, and 4).
m n a b c Difference between b and c
-----------------------------------------------------------------------------------------------------------
6 1 35 12 37 37 - 12 = 25
7 2 45 28 53 53 - 28 = 25
8 3 55 48 73 73 - 48 = 25
9 4 65 72 97 97 - 72 = 25
Example 3. Determine the number of primitive Pythagorean triples (a, b, c) for which b + c = 81, and then find all of them. From Theorem 6, we know that b + c = (m + n)2, so (m + n)2 = 81, m + n = 9, and m = 9 - n. Since m and n are positive integers of opposite parity with no common factors and m > n, we see that there are only three possibilities for m and n as shown below, together with their corresponding triples.
m n a b c Sum of b and c
------------------------------------------------------------------------------------------------------------
8 1 63 16 65 16 + 65 = 81
7 2 45 28 53 28 + 53 = 81
5 4 9 40 41 40 + 41 = 81
Factors of a, b, and c.
But, we are not through! Look again closely at the values for a, b, and c in Table 1 above. Can you find a single number which is a factor (or divisor) of one of the a’s, b’s, or c’s in each and every triple? Take a few seconds now and try to find it for yourself! And, can you find another number which is a factor of just the a’s or b’s alone in each one of the triples? (Don’t read on until you’ve tried to find these numbers!)
Were you able to see that the number 5 is a factor of one of the a’s, b’s, or c’s, and the number 3 is a factor of either a or b but never c in each of the triples in Table 1? Again, we see the amazing order and symmetry of a primitive Pythagorean triple!
Example 4. Look at the triple (55, 48, 73). Its complexity is astounding!
The sum of the squares of its first two integers, 552 + 482, equals the square of its third integer, 732.
The sum of its last two integers, 48 + 73, is the perfect square 121. Its square root, 11, is a factor of its first integer, 55.
The difference of its last two integers, 73 - 48, is the perfect square 25. Its square root, 5, is a factor of its first integer, 55.
The sum of its third and first integer, 73 + 55 = 128, when divided by 2, is the perfect square 64, whose square root, 8, is a factor of its second integer, 48.
The difference between its third and first integer, 73 - 55 = 18, when divided by 2, is the perfect square 9, whose square root, 3, is a factor of its second integer, 48.
The sum of the first and third integers divided by the second integer, (a + c) /b = (55 + 73) / 48 = 128/48 = 8/3 = m / n, gives us the values of m and n which generate (55, 48, 73); that is, m = 8 and n = 3.
5 is a factor of one of its three integers; namely, its first one, 55.
3 is a factor of one of its first two integers; namely, its second one, 48.
Now, is it always true that 3 is a factor of a or b but not both? Let’s see.
1. a and b cannot BOTH have a factor of 3 because if they did, then by Theorem 3, c would also have a factor of 3, and a, b, and c would thus have a common factor of 3. But, they have NO common factors.
2. Consider any positive integer N. Then, for some integer r,
a) if N has a factor of 3, then it can be written as N = 3r.
b) if N has no factor of 3, then it can be written as N = 3r + 1 or N = 3r + 2. (Note that if N = 3r + 7, for example, then it can be rewritten as N = 3r + (6 + 1) = (3r + 6) + 1 = 3(r + 2) + 1 = 3r1 + 1, which is one of the forms in b) above.)
3. Now, either a has a factor of 3 or it doesn’t. If it does have a factor of 3, our theorem is true. If not, then we must show that b has a factor of 3.
4. We know that a = m2 - n2 = (m + n)(m - n), and if a has no factor of 3, then neither m + n nor m-n can have a factor of 3. Thus, from 2b) above,
m + n = 3r + 1 or 3r + 2 and m - n = 3s + 1 or 3s + 2,
for some integers r and s. Considering all cases for m + n and m - n, we get
Case I. Suppose m + n = 3r + 1 and m - n = 3s + 1.
Subtracting the second equation from the first, we get 2n = 3r - 3s. Substituting this value of 2n into b = 2mn, we get b = 2mn = m(2n) = m(3r - 3s) = m(3)(r - s), which shows that 3 is a factor of b.
Case II. Suppose m + n = 3r + 1 and m - n = 3s + 2.
Adding these two equations, we get 2m = 3r + 3s + 3. Substituting this value of 2m into b = 2mn, we get b = 2mn = (2m)n = (3r + 3s + 3)n = 3(r + s + 1)n, which shows that 3 is a factor of b.
Case III. Suppose m + n = 3r + 2 and m - n = 3s + 1.
Adding these two equations, we get 2m = 3r + 3s + 3. Substituting this value of 2m into b = 2mn, we get b = 2mn = (2m)n = (3r + 3s + 3)n = 3(r + s + 1)n, which shows that 3 is a factor of b.
Case IV. Suppose m + n = 3r + 2 and m - n = 3s + 2.
Subtracting the second equation from the first, we get 2n = 3r - 3s. Substituting this value of 2n into b = 2mn, we get b = 2mn = m(2n) = m(3r - 3s) = m(3)(r - s), which shows that 3 is a factor of b.
Thus, for every case, if 3 is not a factor of a, then it is a factor of b. It cannot also be a factor of c because if it were, then two of the numbers a, b, and c would have a factor of 3, and by Theorem 3, then all would have that common factor of 3. But this is impossible, since a, b, and c have NO common factors. We have thus proved
Theorem 7a
In a primitive Pythagorean triple (a, b, c) or right triangle with integral sides
a, b, and c, 3 is a factor of either a or b, but not both, and is NOT a factor of c.
________________________________________________________________
We shall now prove in a similar manner that 5 is a factor of either a, b, or c.
1. Only one of the a, b, or c can have a factor of 5, because if any two of the a, b, and c have a factor of 5, then by Theorem 3, all three would have that common factor. But, a, b, and c have NO common factors.
2. Consider any positive integer N. Then, for some integer r,
a) if N has a factor of 5, then it can be written as N = 5r.
b) if N has no factor of 5, then it can be written as N = 5r + 1, N = 5r + 2, N = 5r + 3, or N = 5r +4.
(Note that if N = 5r + 8, for example, then it can be rewritten as N = 5r + (5 + 3) = (5r + 5) + 3 = 5(r + 1) + 3 = 5r1 + 3, which is one of the forms in b) above.)
3. Now, either b has a factor of 5, or it doesn’t. If it does have a factor of 5, we are through, and our theorem is true. So, we must show that if b has no factor of 5, then either a or c has a factor of 5.
4. We know that b = 2mn, and if b has no factor of 5, then none of its factors can have a factor of 5. Now, if m and n have no factors of 5, they must be in one of the forms shown in the table below.
Case m n
-------------------------------------------------------------------------------------------------
I a) 5r + 1, b) 5r + 2, c) 5r + 3, d) 5r + 4 5s + 1
II a) 5r + 1, b) 5r + 2, c) 5r + 3 d) 5r + 4 5s + 2
III a) 5r + 1, b) 5r + 2, c) 5r + 3, d) 5r + 4 5s + 3
IV a) 5r + 1, b) 5r + 2, c) 5r + 3, d) 5r + 4 5s + 4
-------------------------------------------------------------------------------------------------
Case I-a. Suppose m = 5r + 1 and n = 5s + 1.
Then, a = m2 - n2 = (5r + 1)2 - (5s + 1)2 = 25r2 + 10r + 1 - 25s2 - 10s - 1 = 25r2 + 10r - 25s2 - 10s =
5(5r2 + 2r - 5s2 - 2s), and 5 is a factor of a.
Case I-b. Suppose m = 5r + 2 and n = 5s + 1.
Then, c = m2 + n2 = (5r + 2)2 + (5s + 1)2 = 25r2 + 20r + 4 + 25s2 + 10s + 1 = 25r2 + 20r + 25s2 + 10s + 5 = 5(5r2 + 4r + 5s2 + 2s + 1), and 5 is a factor of c.
Case II-d. Suppose m = 5r + 4 and n = 5s + 2.
Then, c = m2 + n2 = (5r + 4)2 + (5s + 2)2 = 25r2 + 40r + 16 + 25s2 + 20s + 4 = 25r2 + 40r + 25s2 + 20s + 20 = 5(5r2 + 8r + 5s2 + 4s + 4), and 5 is a factor of c.
We have proved 3 of the 16 cases listed above. The other 13 cases may be proved in exactly the same manner as these three, and their proofs are left for the reader’s enjoyment. Thus, we have proved the following theorem.
Theorem 7b
In a primitive Pythagorean triple (a,b,c), or right triangle with integral sides
a, b, and c, 5 is a factor of one and only one of the a, b, or c.
_____________________________________________________________
So, 3 is a factor of a or b (but not both) and not a factor of c, and 5 is a factor of just one of the a, b, or c. But what about b itself? We know that b = 2mn, where m and n are of opposite parity. Thus, one of the m or n is odd and the other is even. Let’s say the n is even. Then, n = 2j for some integer j, and we have b = 2mn = 2m(2j) = 4mj, showing us that b has a factor of 4. Summarizing, we have
3 is a factor of a or b, but not c, 4 is a factor of b, 5 is a factor of just one of the a, b, or c.
Now, consider the product ab. Either a or b has a factor of 3; let’s say it is a. Then a = 3j for some integer j. Also, b has a factor of 4, so b = 4k for some integer k. Then, ab = (3j)(4k) = 12jk, showing us that ab has a factor of 12 !
Consider the product abc. One of the a, b, or c has a factor of 5; let’s say it is c. Then, c = 5r for some integer r. So, abc = (3j)(4k)(5r) = 60jkr, which means that abc has a factor of 60!
Thus, we have
Theorem 8
In a primitive Pythagorean triple (a, b, c), 12 is a factor of ab, and 60 is a factor of abc.
In a primitive right triangle the product of the lengths of its two legs is divisible by 12,
and the product of the lengths of its three sides is divisible by 60.
_______________________________________________________________________________
Example 5. Consider (39, 80, 89). 3 is a factor of a = 39 = 3(13), 4 is a factor of b = 80 = 4(20), 5 is a factor of b = 80 = 5(16), 12 is a factor of ab = 3120 = 12(260), and 60 is a factor of abc = 277,680 = 60(4628).
Example 6. In a certain primitive right triangle, a) the product of the lengths of its three sides is 2040, b) the product of the lengths of its two legs is 120, and c) the length of its hypotenuse is 2 more than its odd leg. Find the lengths of all three sides. From a) and b), we know that abc = 2040 and ab = 120. Thus, substituting 120 for ab, we have abc = (ab)c = 120c = 2040. Solving for c in the last equation, we get c = 17. From c) we know that c = a + 2 or 17 = a + 2. Thus, a = 15. Finally, from b) we know that ab =120. Substituting a = 15 into this last equation, we get 15b = 120 or b = 8
.
6. Areas and Perimeters of Complete Right Triangles
Now, let’s take a look at Table 2 below, which lists the perimeters of various primitive right triangles.
Table 2. Primitive Right Triangles
a b c Perimeter
m n m2 - n2 2mn m2 + n2 a+b+c
-----------------------------------------------------------------------------------------------------
2 1 3 4 5 12 = 3x4
3 2 5 12 13 30 = 5x6
4 1 15 8 17 40
4 3 7 24 25 56 = 7x8
5 2 21 20 29 70
5 4 9 40 41 90 = 9x10
6 1 35 12 37 84
6 5 11 60 61 132 = 11x12
7 2 45 28 53 126
7 4 33 56 65 154
7 6 13 84 85 182 = 13x14
8 1 63 16 65 144
8 3 55 48 73 176
8 5 39 80 89 208
8 7 15 112 113 240 = 15x16
9 2 77 36 85 198
9 4 65 72 97 234
9 8 17 144 145 306 = 17x18
10 1 99 20 101 220
----------------------------------------------------------------------------------------------------
Notice that some of the perimeter values can be written as a product of two consecutive integers, and this apparently happens only when m is 1 greater than n. In section 5, we showed that if m = n + 1, then c = b + 1, and we called any primitive Pythagorean triple with c = b + 1, a complete Pythagorean triple. Similarly, we shall call any primitive right triangle a complete right triangle whenever the length of its hypotenuse is one more than the length of its even leg; that is, whenever c = b + 1 (or equivalently, m = n + 1).
The perimeter P of a primitive right triangle is given by P = a + b + c. Substituting the values of a, b, and c from the formulas of Theorem 5 into P, we get
P = a + b + c = (m2 - n2) + 2mn + (m2 + n2) = 2m2 + 2mn = 2m(m + n). (1)
Now, if we have a complete right triangle, then m = n + 1, and substituting this into equation (1), we have
P = 2m(m + n) = 2(n + 1)(n + 1 + n) = (2n + 2)(2n + 1) = (2n + 1)(2n + 2), (2)
which indeed is a product of two consecutive integers. Furthermore, since m = n + 1, then
a = m2 - n2 = (n+1)2 - n2 = n2 + 2n + 1 - n2,
or a = 2n +1, (3)
and, by rewriting (2) and then substituting (3) into (2), we get
P = (2n + 1)(2n + 1 + 1) = a(a + 1).
Thus, the perimeter P of a complete right triangle (c = b + 1) is the product of a and its successor, a+1.
Theorem 9
Any complete right triangle with odd leg a has a perimeter P = a(a + 1).
_____________________________________________________________
Example 1. Use Theorem 9 to find the perimeter of a right triangle with a = 7, b = 24, and c = 25. Since c = b + 1, the triangle is complete, and P = a(a+1) = 7(8) = 56.
Example 2. Find the perimeter of a right triangle with a = 33, b = 56, and c = 65. Since c ¹ b + 1, we must use
P = a + b + c = 33 + 56 + 65 = 154.
Now, notice that equation (3) tells us that in a complete Pythagorean triple (a. b, c) or complete right triangle,
a = 2n + 1, which is an odd integer (it is in the form 2k + 1). Since n may be any positive integer, then a may be any odd positive integer greater than 1. Thus, for each odd positive integer a greater than 1, there will be a complete right triangle or Pythagorean triple containing this a as a member.
To find the value of b, we simply substitute c = b + 1 into a2 + b2 = c2 and solve for b, giving us a2 + b2 =
(b + 1)2, a2 + b2 = b2 + 2b + 1, a2 = 2b + 1, and thus b = (a2 – 1)/2, giving us the following very useful theorem.
Theorem 10
In a primitive Pythagorean triple (a,b,c) or right triangle with sides a, b, and c,
the value of a may be any odd positive integer greater than 1. For any given
value of a, a complete Pythagorean triple or right triangle having this a as a
member may be found by using b = (a2 - 1)/2, and c = b + 1.
______________________________________________________________
Note that Theorem 10 provides us only with triangles or triples where c is one greater than b; that is, with complete right triangles or triples. This is so because it was proved using m = n + 1.
Example 1. Find the lengths of the sides of a complete right triangle whose perimeter is 56. Since the triangle is complete, the perimeter P = a(a+1) by Theorem 9. Thus, a(a+1) = 56, a2 + a = 56, a2 + a – 56 = 0,
(a – 7)(a + 8) = 0, and a = 7. From Theorem 10, we get b = (a2 – 1)/2 = (72 – 1)/2 = 24, and c = b + 1 = 25. Thus, the lengths are 7, 24, and 25.
Example 2. Find a complete right triangle with one leg of length 35. Since 35 is an odd positive integer greater than 1, we may use Theorem 10 with a = 35, b = (a2 - 1)/2 = (352 - 1)/2 = (1225 -1)/2 = 612, and c = b + 1 = 613. The complete right triangle has sides with lengths of 35, 612, and 613. The associated Pythagorean triple is (35, 612, 613). Now if we look in Table 2 above, we find that (35, 12, 37) is another primitive Pythagorean triple or right triangle with an a-value of a = 35, so (35, 612, 613) and (35, 12, 37) are both primitive Pythagorean triples with a = 35. The formulas of Theorem 10 gave us only ONE of them; namely, the complete one where c = b + 1. This clearly shows that for some values of a, there may be more than one primitive right triangle or Pythagorean triple containing that value. How to find all primitive Pythagorean triples having a given value of a is discussed in the article More Patterns In Pythagoras..
Let’s now take a look at Table 3 below, where we have listed the area A, the perimeter P, and the ratio of the area to the perimeter, A/P, for all complete triangles from n = 1 to 8. Can we find any patterns here?
Table 3. Areas and Perimeters of Complete Right Triangles
a b c Area Perimeter Ratio
m n m2 - n2 2mn m2 + n2 ab/2 a+b+c A / P
--------------------------------------------------------------------------------------------------------
2 1 3 4 5 6 12 6 / 12 = 1/2
3 2 5 12 13 30 30 30 / 30 = 2/2
4 3 7 24 25 84 56 84 / 56 = 3/2
5 4 9 40 41 180 90 180 / 90 = 4/2
6 5 11 60 61 330 132 330 / 132 = 5/2
7 6 13 84 85 546 182 546 / 182 = 6/2
8 7 15 112 113 840 240 840 / 240 = 7/2
9 8 17 144 145 1224 306 1224 / 306 = 8/2
--------------------------------------------------------------------------------------------------------
Yes, there are some patterns. Notice that all the denominators of the ratio A/P are 2, and that the numerator of the ratio A/P of each triple is equal to the value of n for that triple! Thus, we conjecture that
A/P = n/2, (4)
To prove this, we have A = ab/2 = (m2 – n2)(2mn) / 2 = (m + n)(m – n)(2mn) / 2 . (5)
Since the triangle is complete, we know that m = n+1, or equivalently, m – n = 1, so (5) becomes
A = (m + n)(m – n)(2mn) / 2 = (m + n)(1)(2mn) / 2 = 2mn(m + n) /2 = n[2m(m + n)] / 2. (6)
From (1), we have P = 2m(m + n), so (6) becomes, A = n[P]/2 = (n/2)P,
or A/P = n/2, which is (4) above.
To find n for any complete triple, we use a = 2n + 1 from (3), and, solve this equation for n to get
n = (a – 1)/2. Thus, A / P = n / 2 = [(a -1)/2]/2 = (a -1)/4, and we have proved
Theorem 11
For any complete right triangle with sides a, b, and c, the ratio of its area to the
perimeter P is given by A/P = n/2, where n = (a – 1)/2. Thus, A/P = (a – 1)/4.
__________________________________________________________________
Example 3. Find the three sides of a complete right triangle whose area is thrice its perimeter. We know that the triangle’s area A is thrice its perimeter, so A = 3P, or A/P = 3. By Theorem 11, A/P = n/2, so 3 = n/2, or n = 6. Since the triangle is complete, m = n + 1 = 7, and the m- and n- values are 7 and 6, respectively, giving us a = m2 – n2 = 72 – 6 2 = 13, b = 2mn = 2(7)(6) = 84, and c = b + 1 = 85. Thus, the three sides of the complete triangle are 13, 84, and 85.
In More Patterns In Pythagoras, we investigate in great detail the properties which the values of a, b, and c must have in order to be members of primitive right triangles or Pythagorean triples, and we find out how many primitive Pythagorean triples or right triangles are associated with each given value of a, b, or c.
But, before we stop, let’s summarize what we have discovered about the beauty and complexity of these primitive Pythagorean triples and right triangles by looking at two final examples.
Example 4. The primitive Pythagorean triple (21, 20, 29), as was shown in section 5, is NOT complete. Find another triple with a = 21 and check it for completeness. Now (21, 20, 29) is not complete because c is NOT one greater than b, but by using Theorem 10, we can find another triple which is complete. Accordingly, using Theorem 10, we get a = 21, b = (a2 - 1)/2 = (212 - 1)/2 = (441 -1)/2 = 220, and c = b + 1 = 220 + 1 = 221. This gives us (21, 220, 221), and since c = b + 1, it is complete; that is, the sum of b and c is 441, whose square root, 21, equals a.
Example 5. For a complete right triangle with hypotenuse of length 41, find a) its remaining sides, b) its perimeter, area to perimeter ration, and area, and c) the properties of its associated Pythagorean triple.
a) We are given that the length of the hypotenuse is c = 41. Since the triangle is complete, we know that c = b + 1 or b = c – 1 = 40. From Theorem 10, b = (a2 -1)/2, or 40 = (a2 - 1)/2, 80 = a2 - 1, 81 = a2, and a = 9. Thus, its two remaining sides are a = 9 and b = 40.
b) Since the triangle is complete, its perimeter is P = a(a + 1) = 9(10) = 90, by Theorem 9. Its area to perimeter ratio is A / P = (a-1)/4 = (9-1)/4 = 2, by Theorem 11. Since A /P = 2, then its area A = 2P = 2(90) = 180.
c) (9, 40, 41) is its associated Pythagorean triple. Its properties are:
92 + 402 = 412
3 is a factor of a = 9; 5 is a factor of b = 40.
b + c = 81, whose square root, 9, equals a, confirming that (9, 40, 41) is complete.
c - b = 1, whose square root, 1, is a factor of a.
The sum of c and a is 50. Half of this sum, 25, is a perfect square, whose square root, 5, is a
factor of b = 40.
The difference of c and a is 32. Half of this difference, 16, is a perfect square, whose square
root, 4, is a factor of b = 40.
12 is a factor of ab = 9(40) = 360, and 60 is a factor of abc = 9(40)(41) = 14,760 = 60(246).
The sum of the first and third integers divided by the second integer, (a + c) /b = (9 + 41)/40 =
50/40 = 5/4 = m / n, which gives us the values of m and n which generate (9, 40, 41); that is,
m = 5 and n = 4.
In conclusion, we can certainly say that our study has given us richly rewarding glimpses into the beauty, complexity, and order of these wonderful right triangles and Pythagorean triples.
References
[1] Eves, Howard, An Introduction to the History of Mathematics, 3rd ed., New York:
Holt, Rinehart, and Winston, Inc., 1969.
[2] Rademacher, Hans, and Otto Toeplitz, The Enjoyment of Mathematics, tr. by Herbert
Zuckerman, Princeton, New Jersey: Princeton University Press, 1957, pp. 88 - 92
[3] Courant, Richard, and Herbert Robbins, What is Mathematics?, New York: Oxford University
Press, 1941, pp. 40-41
[4] Schaumberger, Norman, Pythagorean Triplets, Quadruplets, . . . , Mathematics in College,
City University of New York, Winter 1983, pp. 36-37.
General Reading
Ball, W. W. Rouse, Mathematical Recreations & Essays, revised by H. S. M. Coxeter,
American Ed., New York: The Macmillan Company, 1947, pp. 57-58