Euclid’s Proof of the Pythagorean Theorem
David W. Hansen
2009
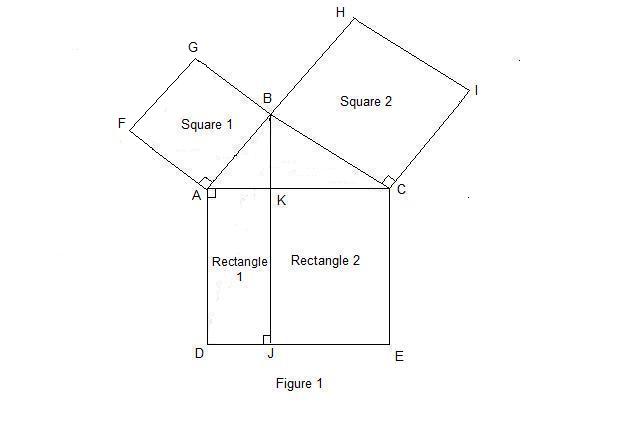
The Pythagorean Theorem states that the sum of the areas of the squares on the two legs of a right triangle equals the area of the square on its hypotenuse. In Figure 1 below, Triangle ABC is a right triangle, AFGB, BHIC, and ADEC are squares, and BJ is perpendicular to DE.
To prove the Pythagorean Theorem, we must show that the sum of the areas of AFGB (Square 1) and BHIC (Square 2) equals the area of ADEC.
Euclid showed that the area of Square 1 equals the area of Rectangle 1, and the area of Square 2 equals the area of Rectangle 2, thus showing that the
Area of Square 1 + Area of Square 2 = Area of Rectangle 1 + Area of Rectangle 2
= Area of Square ADEC.
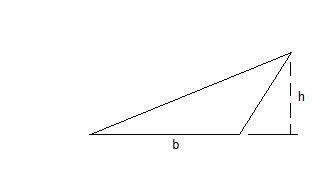
Here’s how he did it. (Recall that the area of the triangle shown below is ½ bh.)
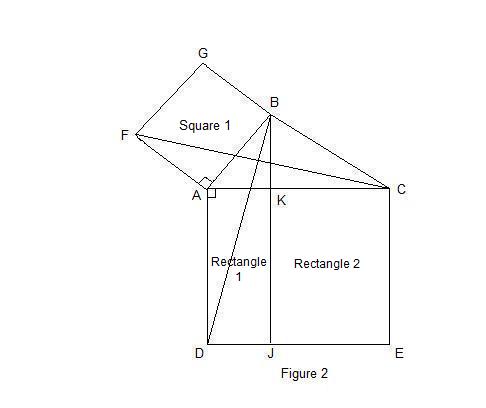
In Figure 2 below, we have
1. The area of rectangle AKJD = AD · DJ, and the area of Triangle ABD = ½ AD · DJ, so
2 · area of Triangle ABD = AD · DJ = area of AKJD. (1)
2. Triangle AFC is congruent to Triangle ABD by SAS because AF = AB, AC = AD,
and angle FAC = angle BAC + 90° = angle DAB. Thus, the
area of Triangle AFC = area of Triangle ABD. (2)
3. The area of Triangle AFC = ½ AF · FG, so 2 · area of Triangle AFC = AF · FG. (3)
Thus, the area of AFGB = AF · FG = 2 · area of Triangle AFC from (3),
= 2 · area of Triangle ABD from (2),
= area of AKJD, from (1).
So, the area of Square 1 = the area of Rectangle 1. (A)
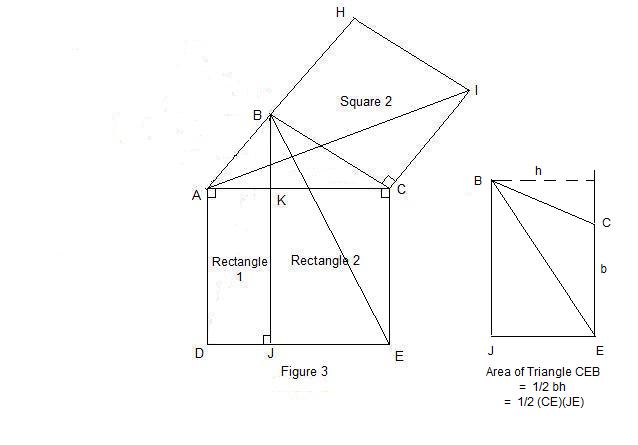
In Figure 3 below, we have
4. The area of rectangle KCEJ = CE · JE, and the area of Triangle CEB = ½ CE · JE, so
2 · area of Triangle CEB = CE · JE = area of KCEJ. (4)
5. Triangle CAI is congruent to Triangle CEB by SAS because AC = CE, CI = BC,
and angle ACI = angle ACB + 90° = angle ECB. Thus, the
area of Triangle CAI = area of Triangle CEB. (5)
6. The area of Triangle CAI = ½ CI · HI, so 2 · area of Triangle CAI = CI · HI. (6)
Thus, the area of BHIC = CI · HI = 2 · area of Triangle CAI from (6),
= 2 · area of Triangle CEB from (5),
= area of KCEJ, from (4).
So, the area of Square 2 = the area of Rectangle 2. (B)
From (A) and (B), we get Area of Square 1 + Area of Square 2
= Area of Rectangle 1 + Area of Rectangle 2
= Area of ADEC,
or: The Pythagorean Theorem
The sum of the areas of the squares on the two legs of a right triangle
equals the area of the square on its hypotenuse.
________________________________________________________
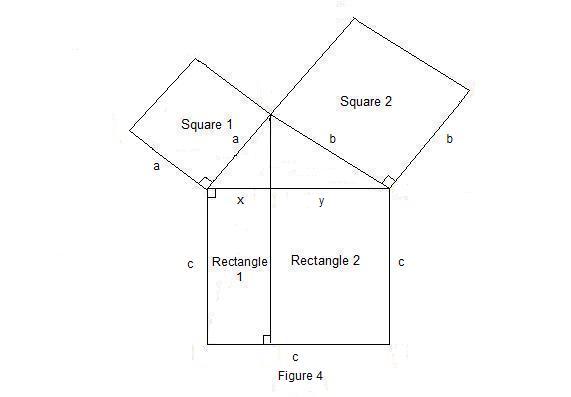
Now, let’s find the dimensions of rectangles 1 and 2, In figure 4 below, we have a right triangle whose legs have lengths of a and b and whose hypotenuse is of length c. Both rectangles 1 and 2 have a length of c, and we have denoted the width of rectangle 1 as x and the width of rectangle 2 as y. Now, we have proved above that
(A) area of Square 1 = area of Rectangle 1
or a2 = cx,
and, solving for x, we have x = a2/c.
Thus, Rectangle 1 has a width of a2/c and a length of c.
Also, we have shown that (B) area of Square 2 = area of Rectangle 2,
or b2 = cy,
and, solving for y we have y = b2/c.
Thus, Rectangle 2 has a width of b2/c and a length of c.
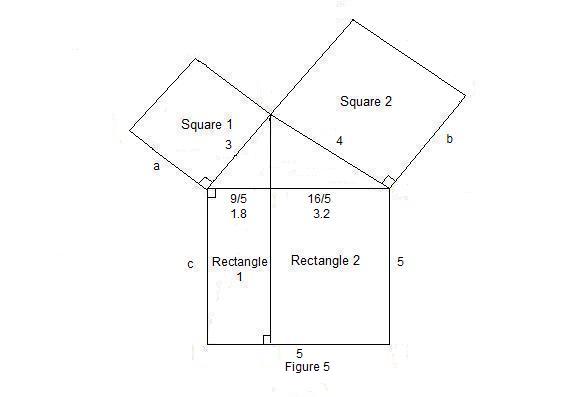
Example. If a = 3, b = 4, and c = 5 as shown in Figure 5 below, then Rectangle 1 has a width of
a2/c = 32/5 = 9/5, and Rectangle 2 has a width of b2/c = 42/5 = 16/5.
Dec 28, 2009